Question

Question 5 (5 points)

Use an inverse matrix to solve the system of equations, if possible.

x + 5y - 3z=-10

-5x + 6y – 5z = -21

-x + 8y - 8z = -25


(1,-1,2)


(-6, -5,2)


(-6, -2,-2)


no solution

Answer 1

Its(1,-1,2)

Explanation:

I took the test

Answer 2

The solution of the system of equations is, (1,-1,2)

Explanation:

Given system equation;

x + 5y - 3z = -10

-5x + 6y – 5z = -21

-x + 8y - 8z = -25

Matrix form is written as;

`\left[\begin{array}{ccc}1&5&-3\\-5&6&-5\\-1&8&-8\end{array}\right] \left[\begin{array}{ccc}x\\y\\z\end{array}\right] = \left[\begin{array}{ccc}-10\\-21\\-25\end{array}\right] \\\\\\det. = 1\left[\begin{array}{cc}\\6&-5\\8&-8\end{array}\right] -5\left[\begin{array}{cc}\\-5&-5\\-1&-8\end{array}\right] -3\left[\begin{array}{cc}\\-5&6\\-1&8\end{array}\right] \\\\\\det. = 1(-8) -5(35)-3(-34)= -8 - 175+ 102 = -81`

Cofactor;

`First \ row \left[\begin{array}{cc}+\\ 6&-5\\\ 8&-8\end{array}\right \left\begin{array}{cc}-\\ -5&-5\\-1&-8\end{array}\right \left\begin{array}{cc}+\\-5&6\\-1&8\end{array}\right] = [-8 \ \ -35 \ \ -34]\\\\\\\ Second \ row \left[\begin{array}{cc}-\\ 5&-3\\\ 8&-8\end{array}\right \left\begin{array}{cc}+\\ 1&-3\\-1&-8\end{array}\right \left\begin{array}{cc}-\\1&5\\-1&8\end{array}\right] = [16\ \ -11 \ \ -13]\\\\\\`

`Third \ row \left[\begin{array}{cc}+\\ 5&-3\\\ 6&-5\end{array}\right \left\begin{array}{cc}-\\ 1&-3\\-5&-5\end{array}\right \left\begin{array}{cc}+\\1&5\\-5&6\end{array}\right]= [-7 \ \ 20\ \ 31]`

`Cofactor =`
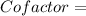
`\left[\begin{array}{ccc}-8&-35&-34\\16&-11&-13\\-7&20&31\end{array}\right]`

`inverse \ matrix =-(1)/(81) \left[\begin{array}{ccc}-8&16&-7\\-35&-11&20\\-34&-13&31\end{array}\right] \\\\\\`

Solution of the matrix:

`\left[\begin{array}{c}x\\y\\z\end{array}\right] = -(1)/(81) \left[\begin{array}{ccc}-8&16&-7\\-35&-11&20\\-34&-13&31\end{array}\right] X \left[\begin{array}{c}-10\\-21\\-25\end{array}\right] = \left[\begin{array}{c}(-8*-10 )/(-81 ) +(16*-21 )/(-81 ) + (-7*-25 )/(-81 )\\\\(-35*-10 )/(-81 ) +(-11*-21 )/(-81 )+ (20*-25 )/(-81 )\\\\(-34*-10 )/(-81 )+ (-13*-21 )/(-81 )+ (31*-25 )/(-81 )\end{array}\right] \\\\\`

`\left[\begin{array}{c}x\\y\\z\end{array}\right] = \left[\begin{array}{c}(-81)/(-81) \\\\(81)/(-81) \\\\(-162)/(-81) \end{array}\right] = \left[\begin{array}{c}1\\-1\\2\end{array}\right]`

Therefore, the correct option is (1,-1,2)