Question

NEED HELP ASAP!! This is a trigonometry question and I really need help, I do not understand it at all. thank you.

Answer 1

AD = 11.87

Explanation:

So first we need to figure out the missing angles.

In ΔBCD, we have two angles given, 40° and 25°, since the angles of a triangle must equal 180°, we need to subtract the sum of these two angles from 180° to find the remaining angle: 180° - (40° + 25°) = 115°

Now we can find the remaining angles in ΔABD. To find ∠D, we can subtract the 115° on the other side from 180° because segment AC is a straight line, which is 180°. This makes that angle 65°. Following the same steps we did before, we can subtract the sum of the two angles in the triangle from 180° to find the remaining angle: 180° - (68° + 65°) = 47°

Now that we have found all the angles, we can start finding the lengths of the segments by using the identity
`(a)/(sin(A))=(b)/(sin(B))=(c)/(sin(C)) =(d)/(sin(D))`

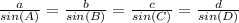
So we only need one segment length, BD, in order to find segment AD. To find segment BD, we can use
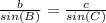`(b)/(sin(B))=(c)/(sin(C))`, in this case
`(DC)/(sin(B))=(BD)/(sin(C))`

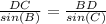
Solving this equation for BD, we get
`(DCsin(C))/(sin(B))={BD}`

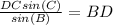
Plugging in the values we have we get
`BD =(15sin(25))/(sin(40)) =9.86`

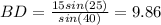
Now we can go over to ΔABD and use
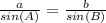`(a)/(sin(A))=(b)/(sin(B))`, in this case
`(BD)/(sin(A))=(AD)/(sin(B))`

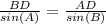
Solving this equation for AD, we get
`(BDsin(B))/(sin(A)) =AD`

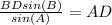
Plugging in the values we have we get
`AD=(9.36sin(68))/(sin(47)) =11.87`

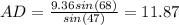
Segment AD = 11.87