Here is the correct format for the question.
Jason and Allison are hiking in the woods when they spot a rare owl in a tree. Jason stops and measures an angle of elevation of 22° 8’ 6”. At the same time, Allison is standing 48 feet closer to the tree, measuring an angle of elevation of 30° 40’ 30” to the owl. If Jason and Allison are the same height, their eyes 5 feet from the ground, find the height of owl in the tree.
Answer:
The height of the owl from the ground is: 67.1337 ft
Explanation:
The first step we are meant to start with is by convert our angle of elevation into degree;
So; we have the given data
22° 8’ 6”
30° 40’ 30”
To degrees ; we get :
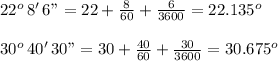
From the attached file below; we can see a diagrammatic representation of the two right angle triangles together showing the data set which include the position of the hikers , the owl on the tree and the angle of elevations.
The trigonometric equations derived from the right angled triangle can be illustrated as:
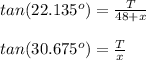
From above equation ;
solving for the value of T , then equating both equations to determine the value of x to find the the height of the owl in the tree; we have:
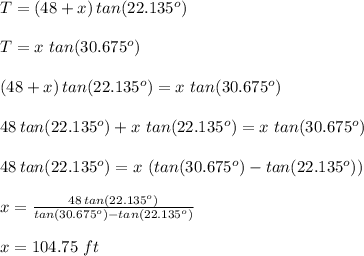
However; to find T; we have:
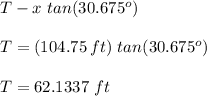
From the question; if we take an integral look and an in depth understanding of the question; we will realize that the value of T = 62.1337 ft is the height the owl is relative to the eye level of the hikers; so if we want to determine the height of the owl from the ground, there is need to add the given (5 feet from the ground) to this number:
SO;
The height of the owl from the ground is: (62.1337 + 5) ft
= 67.1337 ft