Answer:
- Right Triangle-10.5 cm, 20.8 cm, 23.3 cm
- Not a Right Triangle-6 cm, 22.9 cm, 20.1 cm
Explanation:
Given the sets of side lengths of a triangle:
- 10.5 cm, 20.8 cm, 23.3 cm
To verify whether each set of side lengths could be the sides of a right triangle, we use the Pythagorean Theorem. Note that the longest side is always taken as the hypotenuse.
- Pythagoras Theorem:
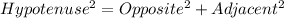
In the set of side lengths 10.5 cm, 20.8 cm, 23.3 cm
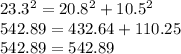
Clearly these satisfies the required theorem and thus are side lengths of a right triangle.
In the set of side lengths 6 cm, 22.9 cm, 20.1 cm
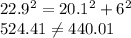
Clearly these does not satisfy the required theorem and thus are not side lengths of a right triangle.