Question

Fill in the missing portions of the function to rewrite g(x) = 3a^2 − 42a + 135 to reveal the zeros of the function. What are the zeros of g(x)? (show your work!)

Enter your answers in the blanks:


g(x) = 3(_____)(_____)


Zeros: ______ and ______

Answer 1

g(x) = 3(x-9)(x-5)

Zeros: x = 9 and x = 5.

Explanation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

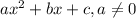This polynomial has roots
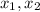`x_(1), x_(2)` such that
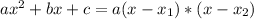`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

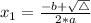
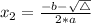
In this question:

`g(x) = 3x^(2) - 42a + 135`

So

`a = 3, b = -42, c = 135`

`\bigtriangleup = (-42)^(2) - 4*3*135 = 144`

`x_(1) = (-(-42) + √(144))/(2*3) = 9`

`x_(2) = (-(42) - √(144))/(2*3) = 5`

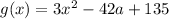
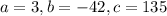
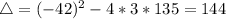
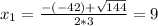
So

g(x) = 3(x-9)(x-5)

Zeros: x = 9 and x = 5.