Question

Rectangle A is a scale drawing of Rectangle B and has 25% of its area. If rectangle A has side lengths of 4 cm and 5 cm , what are the side lengths of rectangle B ?

Answer 1

8 cm and 10 cm

Explanation:

Hello, I can help you with this.

Step 1

According to the question there are two rectangles A and B,

Rectangle A is a scale drawing of Rectangle B and has 25% of its area

in other words

`Area_(A)=0.25*Area_(B) (Equation\ 1)\\`

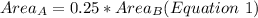
Step 2

Let

Rectangle A

length (1)= 4 cm

length (2)= 5 cm

`Area_(A)=4\ cm * 5\ cm\\Area_(A)=20\ cm^(2)`

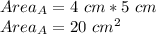
put this value into equation 1

`Area_(A)=0.25*Area_(B) (Equation\ 1)\\\\20\ cm^(2) =0.25*Area_(B) \\divide\ each\ side\ by\ 0.25\\(20\ cm^(2) )/(0.25)=(0.25)/(0.25)*Area_(B)\\ Area_(B)=80\ cm^(2)`

Now, we know the area of rectangle B, to know its length we need to formule other equation

Step 3

`Area_(B)=80\ cm^(2)\\length (1B)*length (2B)=80\ cm^(2) (equation\ 2)\\`

the ratio between the lengths must be constant, so the ratio of A must be equal to ratio in B, then

`(length(1A))/(length(2A))=(length(1B))/(length(2B)) \\\\\\frac{4}{5}= (length(1B))/(length(2B))\\0.8=(length(1B))/(length(2B))\\length(1B)=0.8*length(2B) (Equation 3)`

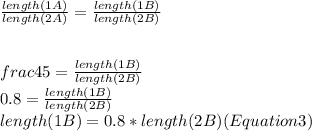
Step three

using Eq 1 and Eq 2 find the lengths

put the value of length(1B) into equation (2)

`length (1B)*length (2B)=80\ cm^(2) (equation\ 2)\\\(0.8*length(2B)) (*length (2B)=80\ cm^(2) \\\\0.8*(length (2B))^(2) =80\ cm^(2)\\(length (2B))^(2) =(80\ cm^(2))/(0.8) \\(length (2B))^(2)=100\\\sqrt{(length (2B))^(2)}=\sqrt{100\ cm^(2)} \\ length (2B)=10\ cm`

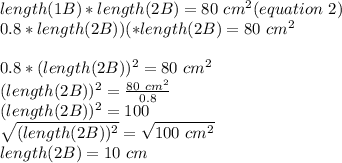
Now, put the value of length(2B) into equation 3 to know length (1B)

`length(1B)=0.8*length(2B)\\length(1B)=0.8*10\ cm\\length(1B)=8 cm`

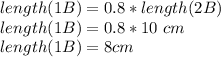
I really hope this helps you, have a great day.