Question

50:19

All else being equal, if you cut the sample size in half, how does this affect the margin of error when using the sample to make a

statistical inference about the mean of the normally distributed population from which it was drawn?

ME.

The margin of error is multiplied by /05

The margin of error is multiplied by 12

The margin of error is multiplied by 05,

The margin of error is multiplied by 2.

Save and Exit

Answer 1

The margin of error is multiplied by 1.41, which is 1 divided by the square root of 5.

Explanation:

The margin of error is:

`M = z*(\sigma)/(√(n))`

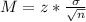
In which z is related to the confidence level,
`\sigma` is the standard deviation of the population and n is the size of the sample.

The margin of error is inverse proportional to the square root of the sample size.

Then

Sample size n:

`M = z*(\sigma)/(√(n))`

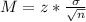
Modified(half the sample size):

`M_(M) = z*(\sigma)/(√(0.5n))`

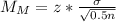
Ratio

`(M_(M))/(M) = (z*(\sigma)/(√(0.5n)))/(z*(\sigma)/(√(n))) = (√(n))/(√(0.5n)) = (√(n))/(√(0.5)*√(n)) = (1)/(√(0.5)) = 1.41`

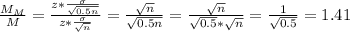
The margin of error is multiplied by 1.41, which is 1 divided by the square root of 5.