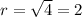Answer:

And solving we got:
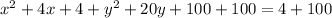
If we subtract 100 from both sides we got:
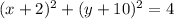

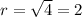
Explanation:
For this case we have the following equation given:

We want to find a general expression given by:
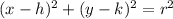
Where the center is (h.k) and the radius is r.
We can begin completing the squares of the equation given and we got:

And solving we got:
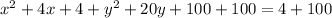
If we subtract 100 from both sides we got:
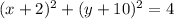
Then we can conclude that the center is:

And the radius would be: