Question

Research indicates the average reaction time to a certain stimulus is 1.47 seconds. Seven subjects have been injected with a drug. Their average reaction time is 1.69 seconds with a standard deviation of .93 seconds. Using a 1% level of significance, does this drug significantly affect the average time to the stimulus?

Answer 1

There is not enough evidence to conclude that the drug significantly affects the average time to the stimulus.

Explanation:

Given:

Mean, u = 1.47

Sample mean, x' = 1.69

Sample size, n = 7

Standard deviation = 0.93

Significance level = 0.01

For null and alternative hypotheses:

H0 : u = 1.47

H1 : u ≠ 1.47

This is a two tailed test.

For the test statistic, tobserved, we have:

`= \frac{\bar{x}-\mu }{(\sigma)/(√(n))}`

`= (1.69-1.47)/((0.93)/(√(7))) = 0.6259 = 0.63`

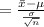
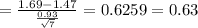
To find the pvalue:

Degree of freedom, df = n - 1 = 7-1 = 6

From table,

Pvalue = 0.5519

For critical value:

The critical value for significance level of 0.01, df = 6, 2 tailed test =

+3.707 & - 3.707

Decision rule: Reject null hypothesis H0, if Tobserved is greater than critical value.

If pvalue is less than significance level we reject H0.

Decision:

We fail to reject null hypothesis H0, since tobserved falls between +3.707 & -3.707.

Since p value 0.5519 is greater than significance level, 0.01, we fail to reject H0.

Conclusion:

There is not enough evidence to conclude that the drug significantly affects the average time to the stimulus.