Given Information:
Loan amount = $280,000
Annual Percentage Rate = APR = 4.4% = 0.044
Number of years = 30
Required Information:
Monthly payment with points = ?
Monthly payment without points = ?
Answer:
Monthly payment with points = $1,361
Monthly payment without points = $1,402.13
Explanation:
The monthly payment can be found using,
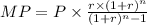
P is the loan amount.
Where interest rate r is given by

Total number of payments n are given by
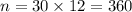
Monthly payment with points:
Rhonda is considering purchasing 2 points and each decreases APR by 0.125%
So the APR becomes
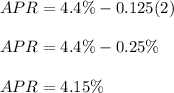
and the corresponding interest rate r is

Finally, the monthly payment is

Monthly payment without points:
Interest rate r is,
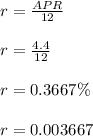
Monthly payment is,

So monthly payment with points is $1,361 and monthly payment without points is $1,402.13