Question

Find the median, first quartile, third quartile, and interquartile range of the data.

203, 183, 212, 181, 157, 204, 189, 190

Median:189, First Quartile:182, Third Quartile:203.5, IQR:21.5

O Median:189.5, First Quartile:182, Third Quartile:203, IQR:21

O Median:189, First Quartile:182, Third Quartile:203, IQR:21

Median:189.5, First Quartile:182, Third Quartile:203.5, IQR:21.5

Answer 1

Median: 189.5

First quartile: 181.5

Third quartile: 203.75

Interquartile Range: 22.25

Explanation:

To find the median, first quartile and third quartile we need to organize the data as:

157, 181, 183, 189, 190, 203, 204, 212

Now, the position of the median is calculated as:

`PosM = (n+1)*(1)/(2)`

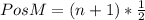
Where n is 8, so replacing we get:

`PosM = (8+1)*(1)/(2)=4.5`

So, the median can be calculated as:

Median = 0.5(189) + 0.5(190) = 189.5

Because 189 is in the fourth position and 190 is in the first position.

At the same way the position for the first and third quartile is:

`PosQ1 = (n+1)*(1)/(4)= (8+1)*(1)/(4)=2.25\\PosQ3 = (n+1)*(3)/(4)= (8+1)*(3)/(4)=6.75`

Then, the first and third quartile is equal to:

Q1 = 0.75(181) + 0.25(183) =181.5

Q3 = 0.25(203) + 0.75(204) = 203.75

Where 181 is in the second position, 183 is the third position, 203 is the sixth position and 204 is the seventh position.

Finally, the interquartile range is calculated as:

Q3 - Q1 = 203.75 - 181.5 = 22.25