Question

7. A, B, C, and D are positive integers. A,B,C forms an arithmetic sequence while B, C, D forms a

geometric sequence. if = , what is the smallest possible value of A+B+C+D

Answer 1

Complete Question

The positive integers A, B, and C form an arithmetic sequence while the integers B, C, and D form a geometric sequence. If (C/B) = (5/3), what is the smallest possible value of A + B + C + D?

Answer:

52

Explanation:

If A, B, and C form an arithmetic progression

Their arithmetic mean,
`B=(A+C)/(2)`

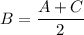
2B=A+C

C= 2B-A

B, C, D forms a geometric sequence and Common ratio, r=C/B=5/3

The terms in the geometric sequence are:

`B, B((5)/(3) ), B((5)/(3) )^2=B, (5B)/(3) , (25B)/(9)`

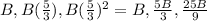
Therefore:

`C=(5B)/(3)\\D= (25B)/(9)`

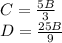
So:

`A, B, C, D=A, B, (5B)/(3) , (25B)/(9)`

From arithmetic sequence

Common difference,
`d=B - A = (5B)/(3) - B`

`2B -(5B)/(3)=A`

`(2 -(5)/(3))B=A\\((1)/(3))B=A\\A=(B)/(3)\\`

`A, B,C, D =(B)/(3),\;B, \;(5B)/(3),\;(25B)/(9)`

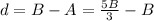
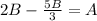
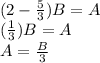
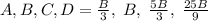
These all have to be positive integers so B must be a multiple of 9, The smallest values are if B is 9

A,B,C,D=3,9,15,25

So the smallest possible value for:

A+B+C+D = 3+9+15+25 = 52