Find the value of each variable in the circle to the right. The dot represents the center of the circle.

Question

asked Mar 17, 2021 120k views

1 Answer

Mabahj · Answer 1 · 2021-03-23T10:22:18+0000

Answer:

Explanation:

According to the inscribed quadrilateral theorem, opposite angles of the quadrilateral are supplementary, which means they sum 180°.

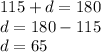
$115+d=180\\d=180-115\\d=65$

Therefore, angle d is 65°.

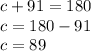
$c+91=180\\c=180-91\\c=89$

Therefore, angle c is 89°.

Now, the angle 115° subtends the arc 99+a, which according to the theorem

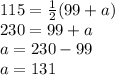
$115=(1)/(2)(99+a)\\ 230=99+a\\a=230-99\\a=131$

Therefore, arc a is 131°.

Similarly, angle c subtends arc a+b, which means

$c=(1)/(2)(a+b)\\ 89=(1)/(2)(131+b)\\ 178=131+b\\b=178-131\\b=47$

Therefore, arc b is 47°.