Question

Se desea construir una letra "ene" mayúscula de tal manera que sus segmentos paralelos midan 25 cm y el

segmento oblicuo que une ambos mida 65 cm. ¿Qué distancia en línea recta separará los segmentos paralelos?

Answer 1

La distancia en línea recta que separa los segmentos paralelos es 60cm.

Explanation:

Esta pregunta se puede resolver usando el teorema de Pitágoras:

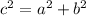`\\ c^2 = a^2 + b^2` [1]

Es decir, en triángulos rectágulos, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos de dicho triángulo. Un triángulo es rectángulo cuando el ángulo que forman sus dos catetos es recto o de 90 grados sexagesimales.

Es importante notar que la letra N tiene dos lados paralelos y el lado oblicuo (o inclinado) une ambos lados paralelos. Pues bien, la letra N puede formar dos triángulos iguales. Escojamos uno de ellos para obtener la respuesta, es decir, la distancia en línea recta que separa los segmentos paralelos (segmentos verticales de la N)

El lado oblicuo (inclinado) es la hipotenusa de ese triángulo (es decir, c). De los catetos, uno está representado por uno de los segmentos paralelos (verticales) de la N (digamos que es b), y, el otro cateto, es la distancia horizontal que une ambos segmentos verticales (digamos que es a).

Si unimos el segmento inferior del cateto b con el extremo inferior de la hipotenusa, se forma el cateto a. Este cateto a forma un ángulo recto con el cateto b y, por lo tanto, forma un triángulo recto. Los lados de un triángulo recto pueden resolverse usando el teorema de Pitágoras, descrito en [1].

Usando [1] y despejando a, tenemos:

`\\ c^2 = a^2 + b^2`

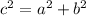
Restamos
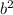`\\ b^2` de ambos lados de la igualdad:

`\\ c^2 - b^2 = a^2 + b^2 - b^2`

`\\ c^2 - b^2 = a^2 + 0`

`\\ c^2 - b^2 = a^2`

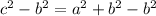
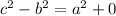
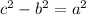
Luego

`\\ a^2 = c^2 - b^2`

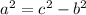
Extrayendo la raíz cuadrada en cada lado de la igualdad:

`\\ √(a^2) = √(c^2 - b^2)`

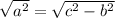
Entonces

`\\ a = √(c^2 - b^2)`

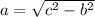
Asimismo, tenemos que
`\\ c = 65`cm y
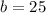`\\ b = 25`cm

Entonces,

`\\ a = √(65^2 - 25^2)`

`\\ a = √(4225 - 625)`

`\\ a = √(3600)`

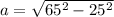
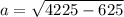
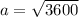
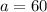`\\ a = 60`cm

De esta manera, el valor de a, o la distancia en línea recta que separa los segmentos paralelos, es 60cm.

Podemos comprobar el resultado anterior haciendo uso del mismo teorema de Pitágoras:

`\\ 65^2 = 60^2 + 25^2`

`\\ 4225 = 3600 + 625`

`\\ 4225 = 4225`

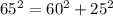
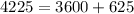
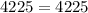
En la figura anexa se aprecia gráficamente lo anteriormente explicado.