Question

Se golpea una pelota de golf de manera que su velocidad inicial forma un ángulo de 45° con la horizontal. La pelota alcanza el suelo a 180 metros del punto en que se lanzó. Calcula su velocidad inicial y el tiempo que ha Estado en el aire

Answer 1

42m/s

6.06s

Step-by-step explanation:

To find the initial velocity and time in which the ball is fling over the ground you use the following formulas:

`x_(max)=(v_o^2sin(2\theta))/(g)\\\\x_(max)=vt_(max)`

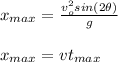
θ: angle = 45°

vo: initial velocity

g: gravitational constant = 9.8m/s^2

x_max: max distance = 180 m

t_max: max time

by replacing the values of the parameters and do vo the subject of the first formula you obtain:

`v_o=\sqrt{(gx_(max))/(sin(2\theta))}\\\\v_o=\sqrt{((9.8m/s^2)(180m))/(sin(2(45\°)))}=42(m)/(s)`

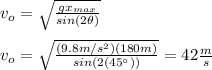
with this value of vo you calculate the max time:

`t_(max)=(x_(max))/(v)=(x_(max))/(v_ocos(45\°))\\\\t_(max)=(180m)/((42m/s)cos(45\°))=6.06s`

hence, the initial velocity of the ball is 42m/s and the time in which the ball is in the air is 6.06s

- - - - - - - - - - - - -- - - - - - - - - - - - - -

TRANSLATION:

Para encontrar la velocidad inicial y el tiempo en el que la pelota está volando sobre el suelo, use las siguientes fórmulas:

θ: ángulo = 45 °

vo: velocidad inicial

g: constante gravitacional = 9.8m / s ^ 2

x_max: distancia máxima = 180 m

t_max: tiempo máximo

reemplazando los valores de los parámetros y haciendo el tema de la primera fórmula que obtiene:

con este valor de vo usted calcula el tiempo máximo:

por lo tanto, la velocidad inicial de la pelota es de 42 m / sy el tiempo en que la pelota está en el aire es de 6.06 s