Question

For the reaction

H2(g) + CO2(g) ⇆ H2O(g) + CO(g)


at 700°C, Kc = 0.534. Calculate the number of moles of H2 that are present at equilibrium if a mixture of 0.680 mole of CO and 0.680 mole of H2O is heated to 700°C in a 70.0−L container.

Answer 1

`n_(H_2)^(equilibrium)=0.393mol`

Step-by-step explanation:

Hello,

In this case, given the amounts of water and carbon dioxide we should invert the given reaction as hydrogen will be producted rather than consumed:

`H_2O(g) + CO(g)\rightleftharpoons H_2(g) + CO_2(g)`

Consequently, the equilibrium constant is also inverted:

`Kc'=(1)/(Kc)=(1)/(0.534) =1.87`

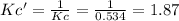
In such a way, we can now propose the law of mass action:

`Kc'=([H_2][CO_2])/([H_2O][CO])`

And we can express it in terms of the initial concentrations of the reactants and the change
`x` due to the reaction extent:

`Kc'=((x)(x))/(([H_2O]_0-x)([CO]_0-x))=1.87`

Thus, we compute the initial concentration which are same, since equal amount of moles are given:

`[H_2O]_0=[CO]_0=(0.680mol)/(70.0L)=0.0097M`

Hence, solving for
`x` by using the quardratic equation or solver, we obtain:

`x_1=0.00561M\\x_2=0.0361M`

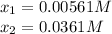
For which the correct value is 0.00561M since the other one will produce negative concentrations of water and carbon monoxide at equilibrium. Therefore, the number of moles of hydrogen at equilibrium for the same 70.0-L container turn out:

`n_(H_2)^(equilibrium)=0.00561mol/L*70.0L=0.393mol`

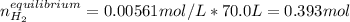
Best regards.