Answer:
The maximum area is 625 square meters.
Explanation:
We know that the area is determined by
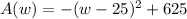
To find the maxium area, we need to calculate the derivative of this function

Then, we make it equal to zero, to find a maxium value
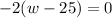
Now, we solve for

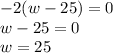
But, according to the problem, the perimeter is 100 meters, because the fencing represents a perimeter.
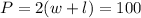
And,
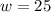
So,
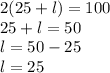
So, the maxium width is 25 meters, the maxium length is 25 meters, and the maxium area is the product of these dimensions
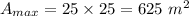
Therefore, the maximum area is 625 square meters.