Answer:
6 ft longer (total length of 15ft)
Explanation:
the initial dimensions are:
length:
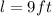
width:
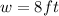
the area area of the garden is given by:
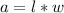
so the original area is:
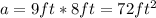
Since we need the area to be
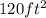 , and we can only change the length, the width will still be 8ft.
, and we can only change the length, the width will still be 8ft.
We substitute the value of the new area and the width to the equation for the area:
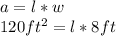
and we clear for the new length:
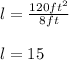
The length of the garden for the area to be
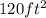 , must be 15ft.
, must be 15ft.
This means that if originally the length was 9 ft, now it has to be 6 ft longer.