Answer:
0.182 probability that the Yankees will win when they score fewer than 5 runs
Explanation:
We use the conditional probability formula to solve this question. It is
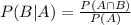
In which
P(B|A) is the probability of event B happening, given that A happened.
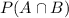 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
In this problem:
When the Yankees score less than 5 runs, either they win, or they lose. The sum of these probabilities is 1.
Probability they lose:
Event A: Scoring fewer than 5 runs.
Event B: Losing
The probability that the Yankees will score 5 or more runs in a game is 0.56.
So 1 - 0.56 = 0.44 probability the Yankees score fewer than 5 runs.
This means that
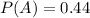
The probability that the Yankees lose and score fewer than 5 runs is 0.36.
This means that
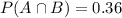
Then the probability they lose is:
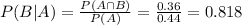
Probability they win:
p + 0.818 = 1
p = 0.182
0.182 probability that the Yankees will win when they score fewer than 5 runs