Question

A 99% confidence interval (in inches) for the mean height of a population is 65.7 < μ < 67.3. This result is based on a sample of size 144.

Construct the 95% confidence interval. (Hint: you will first need to find the sample mean and sample standard deviation).

Answer 1

`66.5 -1.976* 0.3065= 65.89`

`66.5 +1.976* 0.3065= 67.11`

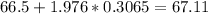
And the 95% confidence interval would be givne by (65.89; 67.11)

Explanation:

For this case we have a 99% confidence interval for the true mean hegiht givne by:

`65.7 \leq \mu \leq 67.3`

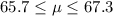
And we can begin finding the mean with this formula:

`\bar X= (65.7 +67.3)/(2)= 66.5`

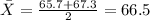
Now we can estimate the margin of error:

`ME = (67.3-65.7)/(2)= 0.8`

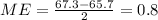
The sample size for this case is
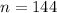`n = 144` then the degrees of freedom are given by:

`df = n-1= 144-1=143`

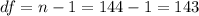
And then we can find a critical value for a 99% of confidence and 143 degrees of freedom using a significance level of 0.01 and we got:

`t_(\alpha/2)= 2.61`

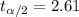
Then the standard error is given by:

`SE = (ME)/(t_(\alpha/2))= (0.8)/(2.61)= 0.3065`

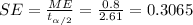
Now we can find the other critical value for 95% of confidence and we got:

`t_(\alpha/2)= 1.976`

And the new confidence interval would be given by:

`66.5 -1.976* 0.3065= 65.89`

`66.5 +1.976* 0.3065= 67.11`

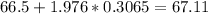
And the 95% confidence interval would be givne by (65.89; 67.11)