Question

Which shows how to find the value of this expression when x = negative 2 and y = 5?StartFraction 3 squared (negative 2) Superscript 6 Baseline Over 5 Superscript 4 EndFraction

StartFraction 3 (negative 2) Superscript 6 Baseline Over 5 Superscript 4 EndFraction

StartFraction 3 squared (5 Superscript 6 Baseline) Over (negative 2) Superscript negative 4 Baseline EndFraction

StartFraction 3 Over (2) Superscript 6 Baseline 5 Superscript 4 Baseline EndFraction

Answer 1

C

Explanation:

Answer 2

StartFraction 3 (negative 2) Superscript 6 Baseline Over 5 Superscript 4 EndFraction

Explanation:

The given values are
`x=-2` and
`y=5`.

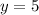The given expression is

`(3x^(3) y^(-2) )^(2)`

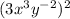
First, we need to multiply exponents

`(3x^(3) y^(-2) )^(2)=3x^(6)y^(-4)`

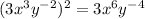
Second, we move the negative exponent to the denominator side

`3x^(6)y^(-4)=(3x^(6) )/(y^(4) )`

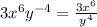
If we replace each value, we have

`(3x^(6) )/(y^(4) )=(3(-2)^(6) )/((5)^(4) )`

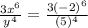
The statement that describes this expression is C.