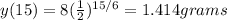Answer:
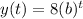 Where b is the decay rate for this case. Using the condition given we have:
Where b is the decay rate for this case. Using the condition given we have:
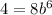
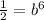

And our model would be given by:
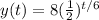
And replacing the value of t=15 we got:
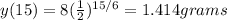
Explanation:
For this case since the half life is 6 hours we have the following condition:

Where
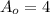 is the initial amount
is the initial amount
Our model for this case is given by this expression:
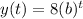 Where b is the decay rate for this case. Using the condition given we have:
Where b is the decay rate for this case. Using the condition given we have:
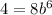
And solving for b we got:
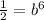
And solving for b we got:

And our model would be given by:
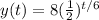
And replacing the value of t=15 we got: