Question

Suppose h#; #i1 and h#; #i2 are inner products on v such that hv;wi1 d 0 if and only if hv;wi2 d 0. prove that there is a positive number c such that hv;wi1 d chv;wi2 for every v;w 2 v.

Answer 1

We take v in the vector space V different from 0. Since v is not 0, then

`< v,v>_1 \, >0 \, ;, <v,v>_2 \, >0`

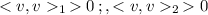
Lets take k>0 such that

`<v,v>_2 \, = k*\, <v,v>_1`

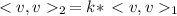
Now, we take any vector w. We want to show that
`<v,w>_2 = k*<v,w>_1` .

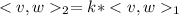Since v is any non-zero vector, then this will prove that
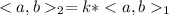`<a,b>_2 = k*<a,b>_1` for any vectors a,b. The reason is that for any vector different from 0, lets name it x, there will exist a constant
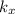`k_x` such that
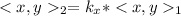`<x,y>_2 = k_x *<x,y>_1` for any y (this is for the same reason a constant exists for v). Since y can be anything, then it can be v. But that means that
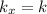`k_x = k`, because v also has its constant k.

Now, lets show that
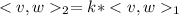`<v,w>_2 = k*<v,w>_1` . Lets take a constant c such that
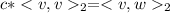`c*<v,v>_2 = <v,w>_2` . We have that

`0 = <v,w>_2 - c* <v,v>_2 = <v, w-cv>_2`

Thus

`<v,w-cv>_1 = 0`

Which means that

`0 = <v,w-cv>_1 = <v,w>_1 - c<v,v>_1`

Which means that
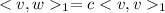`<v,w>_1 = c<v,v>_1` . As a consequence

`<v,w>_2 = c <v,v>_2 = ck*<v,v>_1 = k * <v,w>_1`

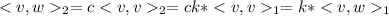
Which proves what we were looking for.