Answer:
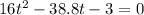
And we can use the quadratic formula given by:
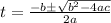
Where:
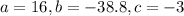
And replacing we got:
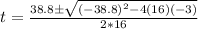
And after solve we got two solutions:
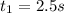
And
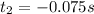
Since the time can't be negative the correct option for this case would be

Explanation:
For this case we have the following function for the height:

And we want to find how many seconds t that the balloon is in the air since is released from 3ft above, so we want to find the time t in order to h(t) =0
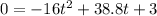
We can rewrite the last expression like this:
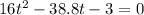
And we can use the quadratic formula given by:
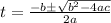
Where:
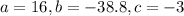
And replacing we got:
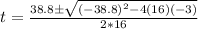
And after solve we got two solutions:
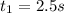
And
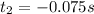
Since the time can't be negative the correct option for this case would be
