Question

Mary has 5 boxes of candy that she wants to hand out as random prizes at her meeting. There are 20 people at her meeting. How many different ways can Mary choose 5 different people to award the candy?

Answer 1

It can be done 15,504 number of ways.

Explanation:

This is a combination problem since we are selecting 5 different people out of a pool of 20people to award the candies. Combination has to do with selection.

Generally, if r people are selected from a pool of n people, this can be done in nCr number of ways.

`nCr = (n!)/((n-r)!r!)`

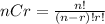
To select 5different people out of 20 people, this can be done in 20C5 ways as shown;

`20C5 = (20!)/((20-5)!5!)\\= (20!)/(15!5!)\\ = (20*19*18*17*16*15!)/(15!*5*4*3*2*1)\\= (19*18*17*16)/(6) \\= 19*3*17*16\\= 15,504ways`

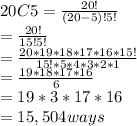
It can be done 15,504 number of ways.