Question

A game advertises, EVERYONE IS A WINNER! It costs $1 to play. You get to choose a card from a standard deck of 52

playing cards. If you choose a red card, you win $3. If you choose a black card, you get $2. What is the expected value of

playing this game?

$1.50

$1.80

-$0.50

$2

Answer 1

`X_(red) = 3, p(red) =(1)/(2)`

`X_(black) = 2, p(red) =(1)/(2)`

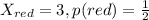
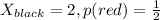
And the cost of play would be 1 with probability 1 for any given game. Then we can find the expected value like this:

`E(X) = 3 *(1)/(2) +2 (1)/(2) -1`

And solving we got:

`E(X) = 1.50`

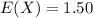
And then the best answer for this case would be:

$1.50

Explanation:

For this case we can calculate the expected value with this formula:

`E(X) =\sum_(i=1)^n X_i P(X_i)`

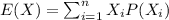
We assume that the standard deck is formed just with red and black cards. For this case we have the following info:

`X_(red) = 3, p(red) =(1)/(2)`

`X_(black) = 2, p(red) =(1)/(2)`

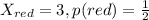
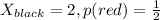
And the cost of play would be -1 with probability 1 for any given game. Then we can find the expected value like this:

`E(X) = 3 *(1)/(2) +2 (1)/(2) -1`

And solving we got:

`E(X) = 1.50`

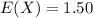
And then the best answer for this case would be:

$1.50