Question

Can anyone tell me the standard form of this parabola equation?

4y^2-x-24y+30=0

And this Circle equation in standard form.
2x^2+2y^2-18x-10y+7=0
​

Answer 1

`x=4y^2-24y+30`

`(x-4.5)^2+(y-2.5)^2=23`

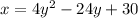
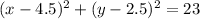
Explanation:

Standard form of a sideways parabola:
`x=ay^2+by+c`

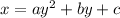
Given equation:

`4y^2-x-24y+30=0`

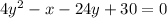
Add x to both sides:

`4y^2-24y+30=x`

`\implies x=4y^2-24y+30`

--------------------------------------------------------------------------------------------

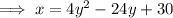
Standard form of circle equation

`(x-a)^2+(y-b)^2=r^2`

(where (a,b) is the center and r is the radius)

Given equation:

`2x^2+2y^2-18x-10y+7=0`

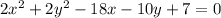
Group like terms:

`2x^2-18x+2y^2-10y+7=0`

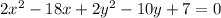
Divide by 2:

`x^2-9x+y^2-5y+3.5=0`

Factor by completing the square for each variable:

`(x-4.5)^2-20.25+(y-2.5)^2-6.25+3.5=0`

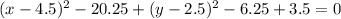
Rearrange into standard form:

`(x-4.5)^2+(y-2.5)^2=23`

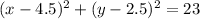
Therefore, the circle has a center at (4.5, 2.5) and a radius of √23