Question

Oil flows into a tank according to the rate F(t)=t^2+1/1+t , and at the same time empties out at the rate E(t)=ln(t+7)/t+2, with both F(t) and E(t) measured in gallons per minute. How much oil, to the nearest gallon, is in the tank at time t = 12 minutes. You must show your setup but can use your calculator for all evaluations. (10 points)

Answer 1

573.95 gallons/minute

Explanation:

To find the amount of oil after 12 minutes you take the difference between the amount of oil that flows into the tank minus the the oil that flows aout the tanks. Then you have:

`T(t)=F(t)-E(t)\\\\F(t)=t^2+(1)/(t+1)\\\\E(t)=(ln(t+7))/(t+2)`

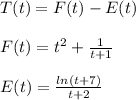
Being F(t) the flow that goes into the tank per minute, and E(t) the amount of oil that flows outside the tank per minute.

To know the total amount of F and E for t=12 you integrate these function:

`\int_0^(12)F(t)dt=(t^3)/(3)+ln(t+1)|_(0)^(12)=578.56(gallons)/(minute)\\\\\int_(0)^(12)E(t)dt=\int_0^(12)[(ln(t+7))/(t+2)]dt=4.61(gallons)/(minute)\\\\\int_0^(12)T(t)dt=578.56-4.61=573.95(gallons)/(minute)`

573.95 gallons/minute