Question

Prices were recorded for all the loaves of bread in a supermarket, the mean price for a loaf of bread was $1.37 with a standard deviation of $0.67, Find the probability that if 13 loaves are selected the mean price is less than $1.00.

A 0.0032


B 0.5643


C 0.9105


D 0.0233

Answer 1

`z = (1-1.37)/((0.67)/(√(13))) = -1.991`

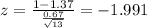
And we want this probability:

`P(z<-1.991)`

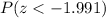
And using the normal standard distribution or excel we got:

`P(z<-1.991)= 0.0233`

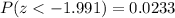
And the best option would be:

D 0.0233

Explanation:

For this case we have the following parameters:

`\mu = 1.37, \sigma =0.67`

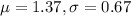
And we select a sample size of n=13. And we want to find this probability:

`P(\bar X <1)`

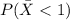
We can assume that the distribution for this case is normal and then we can use the z score formula given by:

`z= (\bar X -\mu)/((\sigma)/(√(n)))`

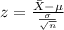
And if we replace the data given we got:

`z = (1-1.37)/((0.67)/(√(13))) = -1.991`

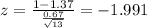
And we want this probability:

`P(z<-1.991)`

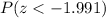
And using the normal standard distribution or excel we got:

`P(z<-1.991)= 0.0233`

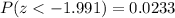
And the best option would be:

D 0.0233