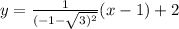There are 2 tangent lines that pass through the point
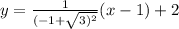
and
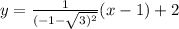
Step-by-step explanation:
Given:
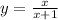
The point-slope form of the equation of a line tells us that the form of the tangent lines must be:
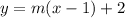
![[1]](https://img.qammunity.org/2023/formulas/mathematics/college/uzec75hi9369kiz2y6cembw3nu31hgqu52.png)
For the lines to be tangent to the curve, we must substitute the first derivative of the curve for
 :
:
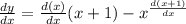

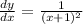
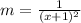
![[2]](https://img.qammunity.org/2023/formulas/mathematics/high-school/2iclaenduq0r0kr577ripnwngioo4x89x3.png)
Substitute equation [2] into equation [1]:
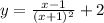
![[1.1]](https://img.qammunity.org/2023/formulas/mathematics/college/e2x1lgpty9x4gwpm1ad4gygnays5h53n06.png)
Because the line must touch the curve, we may substitute
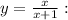

Solve for x:

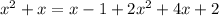
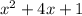
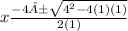
 ±
±

 ±
±

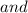
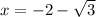
There are 2 tangent lines.
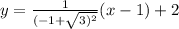
and