Answer:
The amount of moles of CO₂ is 0.026 moles
Step-by-step explanation:
An ideal gas is a theoretical gas that is considered to be composed of point particles that move randomly and do not interact with each other. Gases in general are ideal when they are at high temperatures and low pressures.
The equation known as the ideal gas equation explains the relationship between the four variables P (Pressure), V (Volume), T (Temperature) and n (Amount of substance). The ideal gas law is expressed mathematically as:
P*V = n*R*T
where P represents the pressure of the gas, V its volume, n the number of moles of gas (which must remain constant), R the constant of the gases and T the temperature of the gas.
In this case:
- P= 855 mmHg
- V= 475 mL= 0.475 L
- n= ?
- R= 62.36367
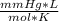
Replacing:
855 mmHg*0.475 L=n*62.36367
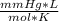 *251 °K
*251 °K
Solving:
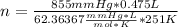
n= 0.026 moles
The amount of moles of CO₂ is 0.026 moles