Answer:
red light > electron > proton > baseball > person > car
Step-by-step explanation:
To calculate the wavelength associated to each object, you use the Broglie's relation:
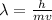
h: Planck,s constant = 6.62*10^-34 Js
m: mass
v: velocity
For each object you use an average values of its mass.
person:
mass = 80kg
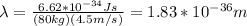
electron:
mass = 9.1*10^{-31}kg
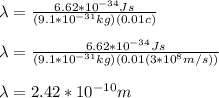
red light:
In this case you use the following formula:
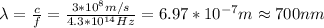
proton:
mass = 1.67*10^{-27}kg
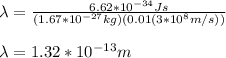
car:
mass = 1500kg
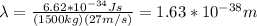
baseball:
mass = 0.145kg
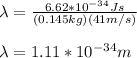
hence, by comparing the wavelengths of the objects you have:
red light > electron > proton > baseball > person > car