Answer:
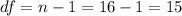
And the significance level is
 and since we are conducting a bilateral test then the critical values are founded with the t distribution with 15 degrees of freedom and we got:
and since we are conducting a bilateral test then the critical values are founded with the t distribution with 15 degrees of freedom and we got:

Explanation:
Information given
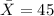 represent the sample mean
represent the sample mean
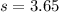 represent the sample standard deviation
represent the sample standard deviation
 sample size
sample size
 represent the value that we want to test
represent the value that we want to test
 represent the significance level for the hypothesis test.
represent the significance level for the hypothesis test.
t would represent the statistic
 represent the p value
represent the p value
System of hypothesis
We want to determine the true mean is 41 per day, the system of hypothesis would be:
Null hypothesis:
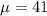
Alternative hypothesis:
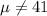
We need to find the degrees of freedom first:
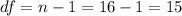
And the significance level is
 and since we are conducting a bilateral test then the critical values are founded with the t distribution with 15 degrees of freedom and we got:
and since we are conducting a bilateral test then the critical values are founded with the t distribution with 15 degrees of freedom and we got:
