Answer:
The length and the width of the new rectangle are 16.5 inches and 6.6 inches respectively
Explanation:
Given
Shape: Rectangle

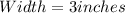

Required
Dimension of the new rectangle
The dimensions of the new rectangle can be solved by multiplying the scale factor by the old dimensions;
This means that
New Length = Scale factor * Old Length
and
New Width = Scale factor * Old Width
Calculating the new length
New Length = Scale factor * Old Length
Substitute 2.2 for scale factor and 7.5 for old length; This gives
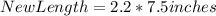
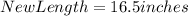
Calculating the new width
New Width = Scale factor * Old Width
Substitute 2.2 for scale factor and 3 for old width; This gives

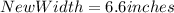
Hence, the length and the width of the new rectangle are 16.5 inches and 6.6 inches respectively