Question

Write an expression for the area of a triangle with a height of 2x^2 units and a base of 5x^2+4x units

Answer 1

The area of the triangle is
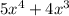`5x^4 + 4x^3` square units

Explanation:

Given

Shape: Triangle

`Height = 2x^2`

`Base = 5x^2+4x`

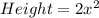
Required

The area of the triangle

The area of a triangle is calculated as thus;

`Area = (1)/(2)(base)(height)`

By substituting
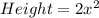`Height = 2x^2` and
`Base = 5x^2+4x`; This gives

`Area = (1)/(2)(5x^2 + 4x)(2x^2)`

`Area = ((5x^2 + 4x)(2x^2))/(2)`

`Area = (5x^2 + 4x)(x^2)`

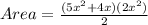
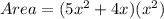
Open Bracket

`Area = 5x^2 * x^2 + 4x * x^2`

`Area = 5x^4 + 4x^3`

Hence, the area of the triangle is
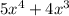`5x^4 + 4x^3` square units