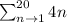Question

Write the series using summation notation.

4 + 8 + 12 + 16 + 20+ . . . + 80

Answer 1

`\sum ^(20) _(n \to \11) 4n`

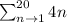
Explanation:

In order to write the series using the summation notation, first we need to find the nth term of the sequence formed. The sequence generated by the series is an arithmetic sequence as shown;

4, 8, 12, 16, 20...80

The nth term of an arithmetic sequence is expressed as Tn = a +(n-1)d

a is the first term = 4

d is the common difference = 21-8 = 8-4 = 4

n is the number of terms

On substituting, Tn = 4+(n-1)4

Tn = 4+4n-4

Tn = 4n

The nth term of the series is 4n.

Since the last term is 80, L = 4n

80 = 4n

n = 80/4

n = 20

This shows that the total number of terms in the sequence is 20

According to the series given 4 + 8 + 12 + 16 + 20+ . . . + 80 , we are to take the sum of the first 20terms of the sequence. Using summation notation;

4 + 8 + 12 + 16 + 20+ . . . + 80 =
`\sum ^(20) _(n \to \11) 4n`