Rationalization:
Rationalising the denominator of the given fraction means we need to multiply both the numerator and the denominator of the fraction by the conjugate of the expression in the denominator. For example:
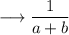
Here the conjugate of denominator of the expression is a - b. So we need to multiply both the numerator and denominator with the fraction.
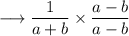
Hence, this is what the rationalization means.
Elucidation:
We have been given and equation and we have been asked to rationalise the equation.
The conjugate of the denominator of the given equation is √(x² + y²) - x. Therefore;
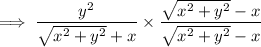
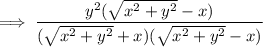
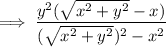

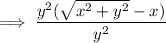
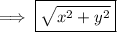
Hence, this is our required solution for this question.