Question:
Find the slope of the tangent to the curve
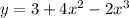 at the point where
at the point where
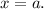
Derivatives:
The derivative of a function can be determined using different rules and formulations. One of the important rules here is the power rule. Power rule is used to differentiate functions in the form of
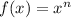 .
.
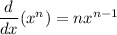
Step-by-step explanation:
We are supposed to find the slope of the tangent to the curve
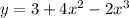 at the point where
at the point where
 .
.


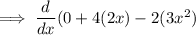

Now plugging
 in the above equation, we obtain the following results:
in the above equation, we obtain the following results:
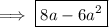
Hence, this is our required solution for this question.