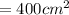Answer:
Area of Shaded Region
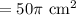
Area of Semicircle
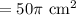
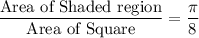
Explanation:
Area of Shaded Region = Area of Sector - Area of Semicircle
Area of Sector
Radius of the sector =20cm
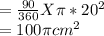
Area of Semicircle
Since AB is the diameter of the semicircle
Radius of the Semicircle=20/2=10cm
Area of semicircle
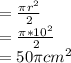
Therefore, area of Shaded Region
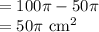
Area of Square =20 X 20