Question

A sphere and a cylinder have the same radius and height. The volume of the cylinder is 21m. what is the volume of the sphere.​

Answer 1

14 m³

Explanation:

We have:

`Cylinder:\\\R-\text{radius}\\H=2R-\text{height}\\V_C-\text{volume};\ V_C=21m^3\\\\\text{the formula of a volume of a cylinder:}\ V=\pi R^2H\\\\V_C=\pi R^2(2R)=2\pi R^3`

`Sphere:\\\R-\text{radius}\\V_S-\text{volume}\\\\\text{the formula of a volume of a sphere:}\ V=(4)/(3)\pi R^3`

`Let's\ transform\ V_C:\\\\2\pi R^3=21\qquad\text{divide both sides by 2}\\\\\pi R^3=(21)/(2)\qquad\text{multiply both sides by}\ (4)/(3)\\\\(4)/(3)\pi R^3=(21)/(2)\cdot(4)/(3)\to V_S=((21:3)\cdot(4:2))/((2:2)\cdot(3:3))=(7\cdot2)/(1\cdot1)=(14)/(1)=14\ (m^3)`

Answer 2

The volume of the sphere is 14m³

Explanation:

Given

Volume of the cylinder =
`21m^3`

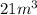
Required

Volume of the sphere

Given that the volume of the cylinder is 21, the first step is to solve for the radius of the cylinder;

Using the volume formula of a cylinder

The formula goes thus

`V = \pi r^2h`

Substitute 21 for V; this gives

`21 = \pi r^2h`

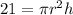
Divide both sides by h

`(21)/(h) = (\pi r^2h)/(h)`

`(21)/(h) = \pi r^2`

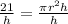
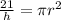
The next step is to solve for the volume of the sphere using the following formula;

`V = (4)/(3)\pi r^3`

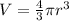
Divide both sides by r

`(V)/(r) = (4)/(3r)\pi r^3`

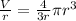
Expand Expression

`(V)/(r) = (4)/(3)\pi r^2`

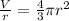
Substitute
`(21)/(h) = \pi r^2`

`(V)/(r) = (4)/(3) * (21)/(h)`

`(V)/(r) = (84)/(3h)`

`(V)/(r) = (28)/(h)`

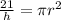
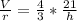
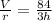
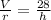
Multiply both sided by r

`r * (V)/(r) = (28)/(h) * r`

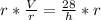
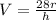`V = (28r)/(h)` ------ equation 1

From the question, we were given that the height of the cylinder and the sphere have equal value;

This implies that the height of the cylinder equals the diameter of the sphere. In other words

`h = D` , where D represents diameter of the sphere

Recall that
`D = 2r`

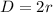
So,
`h = D = 2r`

`h = 2r`

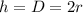
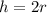
Substitute 2r for h in equation 1

`V = (28r)/(2r)`

`V = (28)/(2)`

`V = 14`

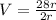
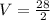
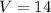
Hence, the volume of the sphere is 14m³