Question

April shoots an arrow upward at a speed of 80 feet per second from a platform 25 feet high. The pathway of the

arrow can be represented by the equation h = -16t2 + 80t + 25, where h is the height and t is the time in
seconds. What is the maximum height of the arrow?
90 feet
140 feet
125 feet
80 feet

Answer 1

The maximum height of the arrow is 125 feet.

Explanation:

The pathway of the arrow can be represented by the equation,

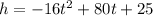`h = -16t^2 +80t + 25` .....(1)

Where h is height in in feet and t is time in seconds.

It is required to find the maximum height of the arrow. For maximum height,
`(dh)/(dt)=0`.

So,

`(d(-16t^2 +80t + 25))/(dt)=0\\\\-32t+80=0\\\\t=(80)/(32)\\\\t=2.5\ s`

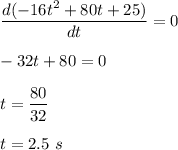
Put t = 2.5 s in equation (1). So,

`h = -16(2.5)^2 +80(2.5) + 25\\\\h=125\ \text{feet}`

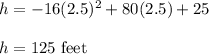
So, the maximum height of the arrow is 125 feet.