Question

A student concluded that the inequality −3+2y≤4x is equivalent to the inequality y≥2x+32, as shown below. Describe and correct the student’s error.

Answer 1

`-3 +2y \leq 4x`

`2y \leq 4x+3`

`y \leq 2x + (3)/(2)`

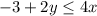
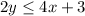
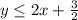
And that's different from the claim of the student that:

`y \geq 2x +(3)/(2)`

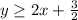
The error of the student is that he/she changes the sign of the inequality from
`\leq` to
`\geq` and that's not possible since we don't multiply both sides of the equation by -1

Explanation:

For this case we have the following inequality:

`-3 +2y \leq 4x`

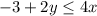
We want to rewrite the last expression with y in the left and x in the right so we can begin adding 3 in both sides of the inequality and we got:

`2y \leq 4x+3`

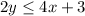
Now we can divide both sides of the inequality by 2 and we got:

`y \leq 2x + (3)/(2)`

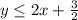
And that's different from the claim of the student that:

`y \geq 2x +(3)/(2)`

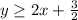
The error of the student is that he/she changes the sign of the inequality from
`\leq` to
`\geq` and that's not possible since we don't multiply both sides of the equation by -1