Question

A thin, uniform, metal bar, 3 m long and weighing 90 N , is hanging vertically from the ceiling by a frictionless pivot. Suddenly it is struck 1.6 m below the ceiling by a small 4-kg ball, initially traveling horizontally at 12 m/s . The ball rebounds in the opposite direction with a speed of 5 m/s. Find the angular speed of the bar just after the collision? Why linear momentum not conserved?

Answer 1

Angular momentum is not conserved in this situation due to the external torque caused by the collision between the ball and the bar. The angular speed of the bar just after the collision can be found using the conservation of linear momentum.

Step-by-step explanation:

Angular momentum is not conserved in this situation because an external torque is acting on the system. The collision between the ball and the bar causes a torque that changes the angular momentum of the bar. The angular speed of the bar just after the collision can be found using the conservation of linear momentum. The linear momentum of the ball just before the collision is equal to the linear momentum of the ball just after the collision. By using the law of conservation of linear momentum and knowing the initial velocity and mass of the ball, you can calculate the final velocity of the ball just after the collision.

Answer 2

w = 1.53 rad / s

Step-by-step explanation:

For this exercise we will use conservation of angular momentum. Let's start by defining our system as formed for the bar and the ball, for which all the torques formed are internal and consequently the angular momentum is conserved.

Initial moment. Just before crash

L₀ = m v₁ L₁

final moment. Right after the crash

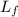`L_(f)` = I_bar w + m v₂ L₁

where L₁ is the distance of the ball L₁ = 1,6m and m its mass 4 kg, let's take as the direction of the positive initial velocity

The moment of inertia of a bar that rotates at its end is

I_bar = ⅓ M L²

L₀ = L_{f}

m v₁ L₁ = (⅓ M L²) w + m v₂ L₁

w = m L₁ (v₁ - v₂) 3 / ML²

let's calculate

velocity v₁ = 1.6 m /s and its bounce v₂ = - 5 m / s

M = W / g

M = 90 / 9.8

M = 9.19 kg

w = 4 1.6 (1.6 + 5) 3 / (9.19 3 2)

w = 1.53 rad / s