Question

Using the following triangle, write a proof to verify that sinA/a=sinC/c

Write two different expressions for h and set the expressions equal to each other

Answer 1

Proved:
`c\sin A=a\sin C\Rightarrow (\sin A)/(a)=(\sin C)/(c)`

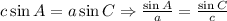
Explanation:

Given: A triangle

To prove:
`(\sin A)/(a)=(\sin C)/(c)`

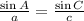
Solution:

Trigonometry is a branch of mathematics that explains relationship between sides and angles of the triangle.

Sine of angle = side opposite to the angle / hypotenuse

In ΔADB,

`\sin A=(BD)/(AB)=(h)/(c)\\\Rightarrow h=c\sin A\,\,\,(i)`

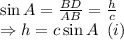
In ΔBDC,

`\sin C=(BD)/(BC)=(h)/(a)\\\Rightarrow h=a\sin C\,\,\,(ii)`

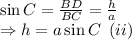
From equations (i) and (ii),

`c\sin A=a\sin C\\(\sin A)/(a)=(\sin C)/(c)`

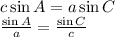
Hence proved