Question

What is the height of a pyramid (with a square base) whose side length is 12 cm and its slant

height is 10 cm?

a.) 22 cm
b.) 8 cm
c.) 2 cm
d.) None of these​

Answer 1

We have been given that side length of pyramid the square base is 12 cm and its slant height is 10 cm. We are asked to find the height of the pyramid.

We will use slant height of a pyramid formula to solve our given problem.

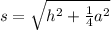`s=\sqrt{h^2+(1)/(4)a^2}`,where,

s = Slant height,

h = Height,

a = Each side of square base.

Upon substituting our given values in above formula, we will get:

`10=\sqrt{h^2+(1)/(4)\cdot 12^2}`

`10=\sqrt{h^2+(1)/(4)\cdot 144}`

`10=√(h^2+36)`

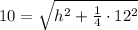
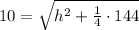
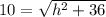
Switch sides:

`√(h^2+36)=10`

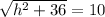
Let us square both sides:

`(√(h^2+36))^2=10^2`

`h^2+36=100`

`h^2+36-36=100-36`

`h^2=64`

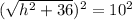
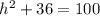
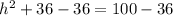
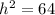
Now we will take positive square root of both sides.

`√(h^2)=√(64)`

`h=8`

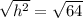
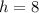
Therefore, the height of the pyramid is 8 cm and option 'b' is the correct choice.