Answer:
The sample size required is 2188.
Explanation:
The (1 - α)% confidence interval for the population proportion is:
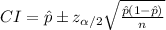
The margin of error for this interval is:
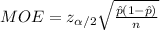
The information provided is:
X = 162
n = 462
MOE = 0.02
Assume the confidence level as 95%.
Compute the sample proportion as follows:
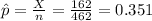
The z-critical value for 95% confidence interval is:
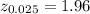
Compute the sample size required as follows:
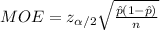
![n=[(z_(\alpha/2)* √(\hat p(1-\hat p)))/(MOE)]^(2)](https://img.qammunity.org/2021/formulas/mathematics/college/wb45wl5kvzkvb20txtpquood16fri70n9o.png)
![=[(1.96*√(0.351(1-0.351)))/(0.02)]^(2)\\\\=2187.781596\\\\\approx 2188](https://img.qammunity.org/2021/formulas/mathematics/college/q9x0onu70kzn9f4sevtsb7inmwdf5zp5i4.png)
Thus, the sample size required is 2188.