Question

Laisha drew a model on grid paper of a decorator tile that she wants to buy. Each grid line represents 5 cm. Her drawing has coordinates (3, 4), (5, 10), (7, 4), and (5, 0). Calculate the area of the real tile.

Answer 1

The area of the real tile is 20 cm².

Explanation:

Plot the points provided on a graph using grid line representing 5 cm each as follows.

The diagram below shows that the model of the tile is in the shape of a kite.

The area of a kite is:

`\text{Area of a Kite}=(p* q)/(2)`

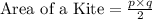
Here, p and q are the two diagonals.

The measure of diagonals p and q are:

p = 10 cm

q = 4 cm

Compute the area of the kite as follows:

`\text{Area of a Kite}=(p* q)/(2)`

`=(10* 4)/(2)\\\\=10* 2\\\\=20`

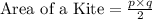
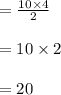
Thus, the area of the real tile is 20 cm².