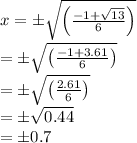Answer:
Option a is correct
Explanation:
Given:
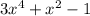
To find: roots of the equation
Solution:
A number x is a root of an equation if it satisfies the equation. It is a real root if it is also a real number.
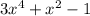
Take
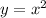

For an equation of the form
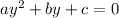 , roots are given by
, roots are given by
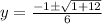
So,
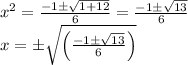
Real zeroes: