Question

Rectangle QUAD has coordinates​ Q(4,5), U(4,10),​ A(11,10), and​ D(11,5). Upper Q prime Upper U prime Upper A prime Upper D primeQ′U′A′D′ is the image of QUAD after a dilation with center​ (0,0) and scale factor 5. What is the length of segment Upper Q prime Upper U primeQ′U′​?

Answer 1

25

Explanation:

Answer: 25

find the length of segment QU.

First, we must find out what the coordinates are.

Q=(4,5) U=(4,10)

Then, Setup your equation by making the first coordinate pair equal. So,

Q= (4,5) would now equal Q=(5,5). That means we added 1. (when you add x ((x=the number you add to make equal)) you add x to the other side as well)

So, now we would add 1 (or how many you got) to U. Thus,

U=(4,10) would now equal Q=(5,10).

Next, set up the equation.

`\sqrt{(Q)^(2) +(U)^(2)` (Q=(5,5) and U=(5,10).)

* You will now be subtracting the coordinates so, Q=(5-5) and U=(5-10)*

Next, Substitute the equation.

`\sqrt{(5-5^(2) +(5-10)^(2)`

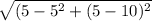
After, we solve.

`\sqrt{0^(2) +(5-10)^(2)`

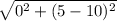
*the sum of two opposites equals 0. 5-5=0*

Next, Subtract (5-10).

`\sqrt{0^(2) +(-5)^(2)`

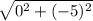
Next, 0 raised to any positive power equals 0

`\sqrt{0+(-5)^(2)`

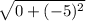
Next, When adding or subtracting 0, the quantity does not change.

`\sqrt{(-5)^(2)`

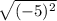
Next, Reduce the index of the radical and exponent 2.

`|-5| = 5`

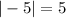
So, The length of segment is 5.

Now, find the length of segment Upper Q'U'​, multiply the length of segment QU by the scale factor.

scale factor in this equation is 5.

Now, multiply.

5·5 = 25

So, the length of segment Q'U' is 25.