Question

The water works commission needs to know the mean household usage of water by the residents of a small town in gallons per day. They would like the estimate to have a maximum error of 0.130.13 gallons. A previous study found that for an average family the variance is 2.562.56 gallons and the mean is 16.316.3 gallons per day. If they are using a 80%80% level of confidence, how large of a sample is required to estimate the mean usage of water? Round your answer up to the next integer.

Answer 1

Therefore, a sample that is required to estimate the mean usage of water must be at least 249.

Explanation:

We are given that they would like the estimate to have a maximum error of 0.13 gallons.

A previous study found that for an average family the variance is 2.56 gallons and the mean is 16.3 gallons per day.

As we know that; Margin of error formula is given by;

Margin of error =
`Z_(_(\alpha)/(2)_) * \text{Standard of error}`

where,
`\alpha` = level of significance = 1 - 0.80 = 20% and
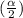`((\alpha)/(2) )` = 10%

Standard of error =
`(\sigma)/(√(n) )`

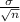
where,
`\sigma` = standard deviation =
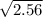`√(2.56)` = 1.6

n = sample size

Also, the critical value of z at 10% significance level is given in the z table as 1.282.

SO, Margin of error =
`Z_(_(\alpha)/(2)_) * (\sigma)/(√(n) )`

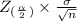
0.13 =
`1.282 * (1.6)/(√(n) )`

`√(n)` =
`(1.282 * 1.6)/(0.13)`

n =
`15.8^(2)`

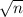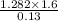
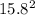
n = 248.95 ≈ 249.

Therefore, a sample that is required to estimate the mean usage of water must be at least 249.